Bending Line Segments into Circles

What we end up with
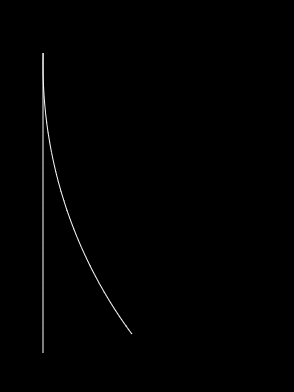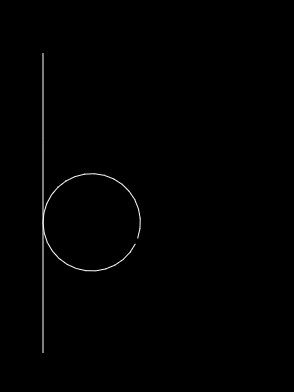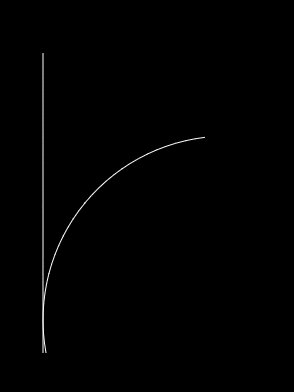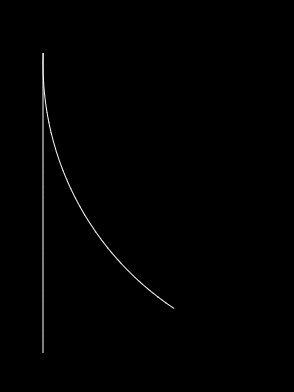
End result
The Problem
Lets say you have a character and you want to make them bend over and touch their toes. You could do that via an animation but that might not be flexible enough for you particular usecase. Maybe you want to change the point the character bends around (e.g. they might get hit at different points on their body in a beat’em up). Let’s say you want to do it procedurally.
That means we want to define a line segment, a pivot point and then bend the line at that point. Also:
- The line should stay exactly the same length all the way through
- We should be able to bend it until the ends touch (and it forms a circle)
The Intuition
We are basically trying to interpolate between two different states. Whenever I have a problem like that, I try to describe both states with the same formula and figure out what factors I can interpolate to get smooth in-between states.
In this case the two states are:
- A line segment (also known as a part of a circle with infinite radius ;) )
- A circle with a circumference as large as the length of the line segment.
As you might have guessed we can describe both states as arc segments on a circle.
From line to circle
So the question is, how do we represent inbetween states?
Radius
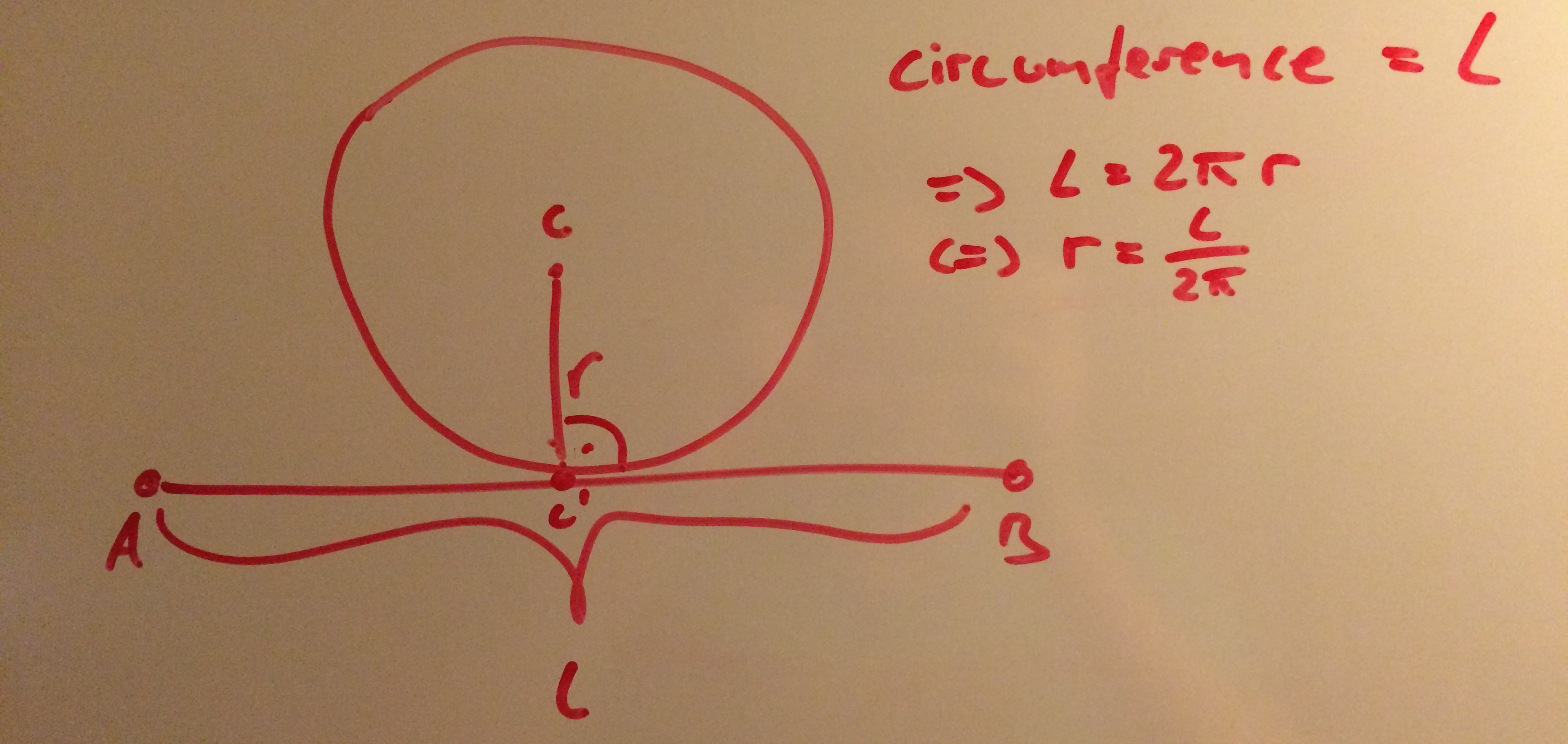
Intuitively, the closer the bent line segment is to a straight line, the larger the radius of the circle. If it’s not bent at all, the radius is infinite. If it’s bent all the way the radius is
$$r = \frac{\text{lineLength}}{2 \pi}$$since
$$ \text{lineLength} = \text{circumference} = 2 \pi r $$A formula that satisfies these requirements is
$$r_{\text{bent}} = \frac{1.0}{\text{bendFactor}} \frac{\text{lineLength}}{2 \pi}$$Segment Length in Radians
The absolute segment length should stay constant, but since the radius is changing, the arc length around the circle in radians has to change as well.
When the line is bent all the way, it wraps around the complete circle. The closer it is to being straight the smaller the angle around the circle has to be. The following works out perfectly:
$$\text{arcLength} = \text{bendFactor} * 2\pi$$In the code below you might notice some other terms. Those are just there to offset the segment around the circle properly and make sure the right parts of the line map to the right parts of the circle.
Pivot
Finally we want to be able to bend the line around a certain point. For that, we just need to move the center of circle along the line to the pivot position and offset the arc segment a little. Both of those are just linear offset and you can see how I implemented that in the code below.
The Code
The function getPosOnBentLine takes parameters describing a bent line and a normalized position t along the line and returns a world space point on the bent line segment.
Note that you can never get a perfectly straight line out of this (passing bendFactor == 0 won’t work because of the division in float circleRad = lineLength / (bendFactor * 2 * PI);). That’s not much of an issue though, since you can either just pass a very small value for bendFactor or switch to a very simple linear interpolation if bendFactor gets close to 0.
/*
Input:
lineStart: Start point of the line segment
lineEnd: End point of the line segment
t: In [0,1], position along the line segment
bendFactor: In (0,1], how bent is the line segment
pivot: In [0,1], position of the bending pivot along the line segment
Returns a point on the bent line
*/
vec2 getPosOnBentLine(vec2 lineStart, vec2 lineEnd, float t, float bendFactor, float pivot) {
vec2 lineDir = lineEnd - lineStart;
float lineLength = length(lineDir);
float circleRad = lineLength / (bendFactor * 2 * PI);
vec2 circleCenter = lineStart + (lineEnd - lineStart) * pivot + perp(lineDir) * circleRad;
float angle = PI + bendFactor * (1.0 - (t+pivot)) * 2 * PI;
vec2 posOnCircle = circleCenter + vec2(cos(angle), sin(angle)) * circleRad;
return posOnCircle;
};
/*
Returns a vector perpendicular to the given value.
*/
vec2 perp(vec2 val) {
return vec2(-val.y, val.x);
}